Graph 3-colorability is NP-Complete

We want to prove that the problem of determining whether or not a graph is 3-colorable is NP-Complete. First, we need to show that it belongs to NP. This is not hard, since all we need to do is to "guess" the color of each vertex. We can then verify that our guess was a 3-coloring of the graph by simply looking at each edge.

Now we need to show how to reduce a problem that is already known to be NP-Complete to the graph 3-colorability problem. The problem we will use is called 3-Satisfiability. It is a version of the Satisfiability problem in which every clause contains exactly 3 variables (possible negated).

We need to show that, given an instance of 3-satisfiability, we can construct an "equivalent" instance of the Graph 3-colorability problem. By equivalent, we mean that:

• We can assign true/false values to every variable in the instance of satisfiability, so that every clause evaluates to true

• We can color the vertices of the graph using 3 colors, such that no edge has both endpoints of the same color.

This allows us to solve the instance of Satisfiability by constructing the graph, and then checking whether or not we can color it. If so, the instance of Satisfiability was satisfiable; if not, it wasn't.

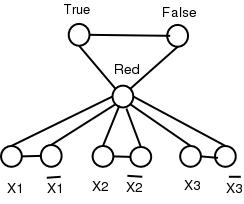
So back to our construction. First, we create a triangle, whose vertices we will call true, false and red. These names will also be the names we will give to the color that gets used for these vertices when the graph is 3-colored. Then for every variable xi that appears in the instance of Satisfiability, we connect a vertex xi to a vertex xi, and we connect both xi and xi to red. This is illustrated below for a case where there are (only) 3 variables.

Now, we will also create a little piece of the graph for each clause. This piece of the graph will look like the one in the figure below. Here, we have drawn one for the clause "x1 or x2 or x3".

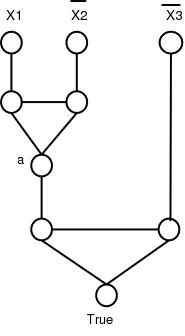
The vertices labeled x1, x2, x3 and true in the figure are the same vertices as those in the first figure (i.e. we only have one each of them in the graph, and they are shared between all the pieces of graphs used for the clauses).

This part of the graph has an interesting property: the only ways to color it with the colors true, false and red, without having an edge whose two endpoints have the same color, is to use the color true for at least one of the vertices at the top. Conversely, if you assign colors true and false to the three vertices at the top, then as long as at least one of them was colored true, then you will be able to color the rest of the graph.

Let us now prove that we can color the graph using 3 colors if and only if the instance of Satisfiability is satisfiable.

• Suppose first that the instance of Satisfiability is satisfiable. That is, we can assign the values true and false to the variables, so that every clause evaluates to true. We can color the graph as follows:
  • If variable xi was assigned the value true, then we color vertex xi true, and vertex xi false. If variable xi was assigned the value false, then we color vertex xi false, and vertex xi true.
  • Clearly we have not colored the two endpoints of any of our edges with the same color yet, and the only vertices that still have to be colored are those inside the pieces of the graphs that are used for each clause. Since every clause is satisfied by our choice of values for the variables, this means that at least one of the three vertices at the top is colored true. Hence we can color the rest of these using the three colors.
• Now suppose that the graph can be colored using 3 colors. We assign the value true to a variable xi if the vertex xi was colored true, and the value false if the vertex xi was colored false (this vertex can not be colored red because it is adjacent to the red vertex). Every clause C must be true, because the piece of the graph used for C can only be colored with 3 colors if one or more of the vertices at the top is colored true. This means that the instance of Satisfiability is satisfiable.

And that's the end of the proof.